This topic is rather long, so I decided to split it into 2 parts. This part will cover the following items:
- statistics concepts
- frequency distribution
- measures on central tendency (mean, median, mode)
1. Concepts:
Descriptive Statistics are used to summarized important characteristics of large data sets.
Inferential Statistics are tools used to draw larger generalizations from observing a smaller portion of data.
A Population is the set of all possible members of a stated group
A Sample is a subset of the population of interest
Parameter is the measure used to describe a characteristic of a population.
Sample Statistics is used to measure a characteristic of a sample.
Types of measurement scales
Level of measurement increases as we move down this list.
Nominal - observations are classified or counted with no particular order. Example: in a living room, number 1 is a table, 2 is a TV, 3 is a vase, etc.
Ordinal - data is categorized according to some rank that helps to describe differences between data. Example: an IQ of 120 ranks higher than an IQ of 100. However, you can't say that the difference between IQs of 140 and 120 is the same as the difference between IQs of 120 and 100.
Interval - like Ordinal scale, this provide relative ranking but the difference between scale values are equal. Example: the difference between 30 and 20 degrees Celsius is the same as the difference between 60 and 50 degree Celsius. However, the weakness of this scale is that a 0 degree Celsius does not mean that there is no temperature. This means that interval-scale-ratios are meaningless.
Ratio - this scale provide ranking, equal difference, and a true zero point. Example: if you have $100, it means that you have 4 times as much as $25; and $0 means that you have no money.
2. Frequency Distribution:
Steps to construct a frequency distribution:
Step 1: Define intervals. Intervals must have lower and upper limits and are mutually exclusive (i.e. 1 observation can only fall to 1 interval). The total set of intervals should cover the total range of values for the entire population.
Step 2: Count the observations to get the Absolute Frequency (i.e. number of observations that fall within a given interval)
Other ways to present data
Relative frequency is calculated by dividing the absolute frequency of each interval by the total number of observations.
Cumulative Absolute Frequency and Cumulative Relative Frequency is the sum of absolute or relative frequencies starting at the lowest and moving up to the highest.
The following examples are taken from Kaplan SchweserNotes 2011 to illustrate the concepts.
The table below represents the returns on Intelco's stock
Annual
Returns for Intelco Stock
|
|||
10.4%
|
22.5%
|
11.1%
|
–12.4%
|
9.8%
|
17%
|
2.8%
|
8.4%
|
34.6%
|
228.6%
|
0.6%
|
5.0%
|
–17.6%
|
5.6%
|
8.9%
|
40.4%
|
–1.0%
|
–4.2%
|
–5.2%
|
21.0%
|
To construct Frequency Distribution for the data above:
Step 1: Define Interval.
The range of return = 69% = 40.4% – (–28.6%). We can use 8 nonoverlapping intervals of 10% Step 2:
Interval
|
Absolute
Frequency
|
Relative Frequency
|
Cumulative Absolute Frequency
|
Cumulative Relative Frequency
|
–30% ≤ Rt < –20%
|
1
|
1/20 = 5%
|
1
|
5%
|
–20% ≤ Rt < –10%
|
2
|
2/20 = 10%
|
3
|
15%
|
–10% ≤ Rt < 0%
|
3
|
3/20 = 15%
|
6
|
30%
|
0% ≤ Rt < 10%
|
7
|
7/20 = 35%
|
13
|
65%
|
10% ≤ Rt < 20%
|
3
|
3/20 = 15%
|
16
|
80%
|
20% ≤ Rt < 30%
|
2
|
2/20 = 10%
|
18
|
90%
|
30% ≤ Rt < 40%
|
1
|
1/20 = 5%
|
19
|
95%
|
40% ≤ Rt < 50%
|
1
|
1/20 = 5%
|
20
|
100%
|
Total
|
20
|
100%
|
The interval with greatest absolute frequency is the 0% ≤ Rt < 10% interval. It is called the Modal Interval.
Histogram and Frequency Polygon are the graphical presentations of the absolute frequency distribution (see picture below)
3. Measures on Central Tendency
Population Mean is calculated is follows
Sample Mean is used to make inferences about the population mean
The population and sample mean are both arithmetic means, which is the sum of observation values divided by the number of observations.
The sum of the deviations from the mean is zero
Weighted mean takes into account the weights of different observations and is computed as follows:
Example: An investor has a portfolio with 35% stocks, 30% bonds, 20% cash, and 15% commodity. Their returns are 15%, 7%, 4%, and 8% respectively. What is the portfolio return?
Portfolio return = weighted mean of the returns = (0.35 x 0.15) + (0.3 x 0.07) + (0.2 x 0.04) + (0.15 x 0.08) = 0.0935, or 9.35%
The return of a portfolio is the weighted average of the returns of the individual assets in the portfolio.
Median is the midpoint of a data set when the data is arranged in ascending or descending order. 50% of the observations are above and 50% are below the median. Median is a better measure of central tendency than arithmetic mean when there are extremely large or small values in the observations.
Example: Find medians of the following sets of data
a. 5, 12, 3, 9, 37
b. 4, 7, 2, 9, 16, 11
a. Arrange the numbers in descending order: 37, 12, 9, 5, 3. Median is 9 because it is the midpoint of the data set.
b. Arrange: 16, 11, 9, 7, 4, 2. With an even number of observations, the median is the arithmetic mean of the 2 middle observations, 9 and 7. Thus, median = (9 + 7)/2 = 8
Mode is the value that occurs most frequently in a data set. A data set may have more than one Mode or no Mode.
A distribution is Unimodal when it has one value that appears most frequently .
When a set of data has 2 or 3 values that occur most frequently, it is said to be bimodal or trimodal.
Geometric mean is computed as follows:
When calculating the geometric mean for a returns data set, it is necessary to add 1 to each value under the radical then subtract 1 from the result as follows:
Example: the returns of a stock over 4 years are 10%, –20%, 5%, and –4% respectively. Compound the annual rate of return over the 4-year period.
1 + RG = [(1 + 0.1)(1 – 0.2)(1 + 0.05)(1 – 0.04)]1/4
= 0.9705
RG = –0.0295
= –2.95%
Harmonic mean is used for calculations such as average cost of shares purchased over time.
Example: an investor purchase $1000 stock each month, and over the past 3 months prices per share were $8, 10$, $5. Calculate the average cost per share.
average cost per share = harmonic mean = 3/(1/8+1/10+1/5) = $7.06








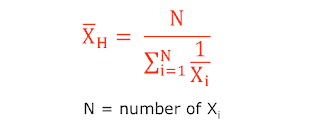
No comments:
Post a Comment